admin

About admin

Posts by :

February 2 2025

nature_paper_sum

source:
Boosting AI with neuromorphic computing Nat Comput Sci 5, 1–2 (2025). https://doi.org/10.1038/s43588-025-00770-4

Neuromorphic computing has the potential to greatly improve the power efficiency, performance, application of AI on the edge.

Types of Artificial intelligence (AI)¶

Large Language Models (LLMs): $\rightarrow$ general human-like conversational agents, such as ChatGPT,

Expert Domain-Specific Tools:

NYUTron (all-purpose clinical prediction engine ),
ChemCrow (Used in organic synthesis, drug discovery, and materials design).

Reasoning AI Models: OpenAI o1 and o3-mini.

Challenge with current AI is in Training and Implementation of large-scale models. Requires state-of-the-art digital processors => computing speed at a high energy cost

limitation arises from the design of conventional digital processors. A phenomenon known as the von Neumann bottleneck, which stems from separating (physically) memory and computing processor.

The von Neumann bottleneck highlights the need for a balanced system design where memory speed, bus bandwidth, and processing power are optimized together

Fundamental to the von Neumann architecture in classical computing, the central processing unit (CPU) and memory are physically separated and communicate through a single data path or bus. Because data and instructions are transferred sequentially over this single bus, the system experiences:

Limited Bandwidth $\Rightarrow$ The data transfer rate is constrained by the bus speed rather than the CPU’s processing capability.
Instructions and Data Fetching $\Rightarrow $ In a von Neumann architecture, instructions and data share the same memory and communication channel, leading to conflicts and delays—especially in modern applications requiring large datasets or parallel processing.

Mitigation Strategies:

Caching: Small, fast memory stores frequently accessed data closer to the CPU
Parallel Processing: Using multiple cores or processors to distribute the workload
Harvard Architecture: Separating data and instruction memory to avoid contention
Increased Bus Bandwidth: Faster or wider buses to move more data simultaneously

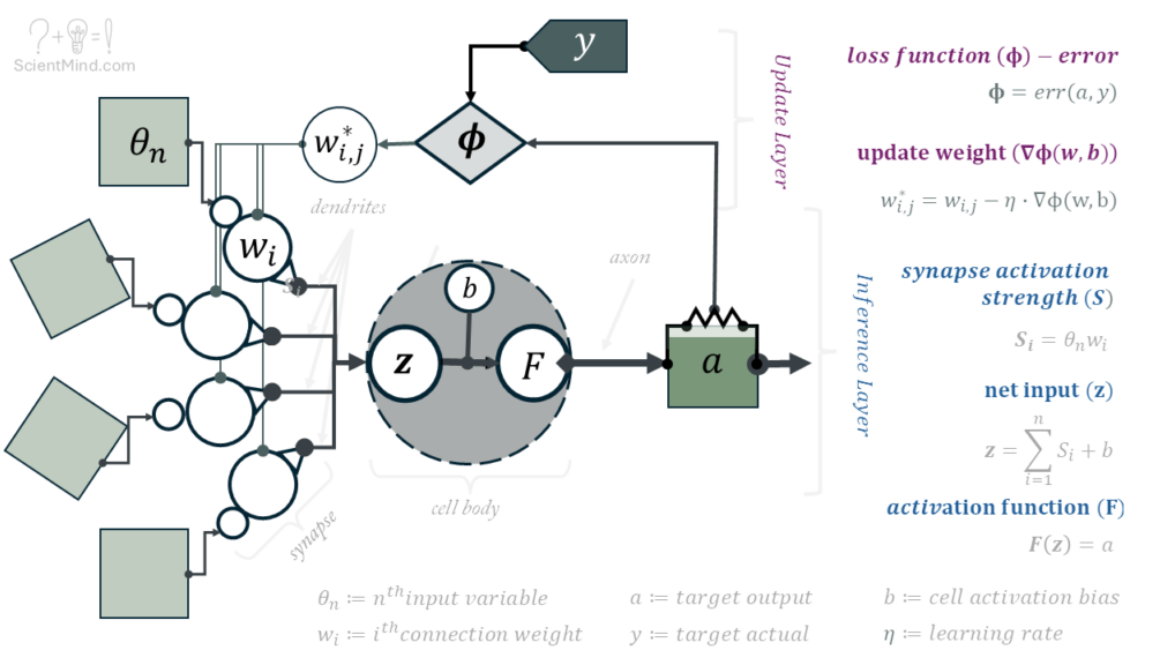
Neuromorphic computers perform computations by mimicking the structure and function of neurons and synapses in the brain

One solution is to redesign computing architecture using Spiking Neural Networks (SNNs) with memristors as neurons. With neuromorphic computing, information processing and memory are collocated and integrated within the SNN, eliminating the energy-costly memory movement step inherent in von Neumann computing architecture.

Challenge with Neuromorphic Computing¶

From October 2024 2nd Nature Conference on Neuromorphic Computing, focusing on the transformative power of neuromorphic computing in advancing AI

Memristors can mimic the human brain’s energy-efficient synapses and neurons, a concept known as in-memory computing (IMC). $\rightarrow$ IMC leverages local memory devices to perform computations, avoiding the energy-intensive step of moving data around.

IMC enables the deployment of AI tasks on local devices—“AI on the edge”—for applications such as:

Autonomous driving
Clinical diagnostics

From Lin, Y., Gao, B., Tang, J. et al. Deep Bayesian active learning using in-memory computing hardware. Nat Comput Sci (2024). https://doi.org/10.1038/s43588-024-00744-y

The authors demonstrate the implementation of Deep Bayesian active learning within the IMC framework using memristor arrays to eliminate extensive data movement during vector–matrix multiplication (VMM).

Additionally, they utilize the intrinsic randomness properties of memristors to efficiently generate random numbers for weight updates during the training of probabilistic AI algorithms. → Reducing time latency and power consumption.

importance of IMC can be further exemplified by

Büchel, J., Vasilopoulos, A., Simon, W.A. et al. Efficient scaling of large language models with mixture of experts and 3D analog in-memory computing. Nat Comput Sci (2025). https://doi.org/10.1038/s43588-024-00753-x

The authors propose a three-dimensional (3D) construction of non-volatile memory (NVM) devices that simultaneously meets memory requirements and addresses the parameter-fetching bottleneck in large LLMs while reducing energy costs. They employed a conditional computing model designed to minimize inference costs and training resources.

Despite the fact that conditional computing on digital processors is notoriously impractical for large-scale models,

authors demonstrated that mapping the conditional computing mechanism onto a 3D IMC architecture can be a promising approach to scale up large models

With the increasing availability of neuromorphic processors, identifying practical applications has become more important than ever. Potential applications include healthcare diagnostics, visual adaptation, and signal processing.

Additionally, the concept of hardware–software co-design (or >algorithm-guided hardware design) is considered essential for fully realizing the benefits of neuromorphic processors across various applications.

At the conference, two key issues were broadly discussed:

Lack of community-acknowledged benchmark datasets $\rightarrow$ Without standardized benchmarks, accurately measuring new technological advancements is challenging. NeuroBench framework aims to address this gap.
Absence of best practices for code sharing $\rightarrow$ Neuromorphic-related source code is often highly dependent on the underlying hardware, making reproducibility and collaboration difficult.

Establishing standardized practices and infrastructures for sharing code and data—while accounting for hardware differences—will be essential for the continued success of neuromorphic computing.

January 21 2025

admin Uncategorized 0

Installation

These python libraries (packages) are required. On install using pip command, these dependencies are installed. nd thus automatically installed when using pip command.

torch >= 1.1.0 ; numpy >= 1.17 ; pandas ; matplotlib ; math ; nir ; nirtorch

In Terminal Command Install
Open Win Menu > type: cmd > enter > a terminal window opens > In window type pip install

> pip install snntorch

In Python file

import torch, torch.nn as nn
import snntorch as snn

Troubleshooting

In Tutorial 1 – torchvision is required – TorchVision is a popular library for computer vision tasks, and it works alongside PyTorch.
Install using terminal command

> pip install torchvision

January 20 2025

admin Neuromorphic Computing & Engineering 0

p4_snnTiorch

INTRODUCTION¶

Learning PyTorch+ssnTorch > Go To Page

A fundamental differences between SNN like in the brain and modern deep learning ANN is that the brain encodes information in spikes of activity rather than a continuous activations or inhibition (Figure 1). Found a python based framework for modelling SNN > called snnTorch, which is based on the ANN framework PyTorch. GOAL :Learning PyTorch + snnTorch > unlocks SNN modelling > Neuromorphic algorithms > applications

Figure 1 – A skematic representation of a SNN neuron receiving input in the form of spikes over a period of time, and responding to that input with with a spike

PyTorch is an optimized tensor library for deep learning using GPUs and or CPUs. Key features include: "GPU acceleration" and "automatic differentiation" capabilities, which as I understand it, will save me time on tedious programming work and makes programming a neural network, Arificial or Spiking, much smoother.

A tensor is a multi-dimensional array, that serves as the fundamental building block for computation in deep learning.

snnTorch is an open-source python library which leverages PyTorch’s tensor operations, GPU acceleration, and automatic differentiation for designing, training, and evaluating spiking neural networks (SSN). It extends PyTorch’s capabilities to include:

Specific tools for simulating, training, and evaluating spiking neurons $\Rightarrow$ SNN Modelling
Offers four Predefined Spiking Neuron Models = {Leaky Integrate-and-Fire (LIF), Hodgkin-Huxley, Adaptive Integrate-and-Fire}
Supports event-driven computations $\Rightarrow$ processing temporal and sparse data efficiently, reducing computational cost and energy usage.
Supports training SNNs using surrogate gradients, a technique that approximates gradients for non-differentiable spiking activation functions.
- At present, neuron models are represented by recursive functions $\rightarrow$ removes the need to store membrane potential traces for all neurons in a system in order to calculate the gradient.
Allows the simulation of spatiotemporal dynamics for tasks involving time-series or event-based data.
Compatible $\Rightarrow$ Integration with PyTorch’s ecosystem.
- designed to be intuitively used with PyTorch, as though each spiking neuron were simply another activation in a sequence of layers.

Note:

lean requirements of snnTorch enable small and large networks to be viably trained on CPU.
Provided the network models and tensors are loaded onto CUDA, snnTorch takes advantage of GPU acceleration in the same way as PyTorch.
my programming skills in python are the basics. But I think I can make my way through by reading the documentation and examples, and using AI assists.

[1] ssnTorch [2] pyTorch [3] chatGPT: "What is snnTorch?"

January 8 2025

admin Cognitive Neuroscience: Memory and Learning 0

date_p3_connectome

Introduction¶

This content is based on #189 of the Mindscape podcast, hosted by Sean Carroll, an American theoretical physicist and professor specializing in quantum mechanics, cosmology, and the philosophy of science. Carroll is currently affiliated with Johns Hopkins University. In this episode, his guest is Dr. Jeff Lichtman, an American neuroscientist and Professor of Molecular and Cellular Biology and Arts and Sciences at Harvard University.

Dr. Lichtman is renowned for developing a groundbreaking neuroimaging technique called Brainbow. When combined with serial electron microscopy, Brainbow enables the creation of detailed 3D reconstructions of a brain’s neural wiring. This comprehensive map of all neural connections, known as a connectome, represents a major advancement in neuroscience, with Dr. Lichtman as one of its pioneering contributors.

The episode delves into four key themes: our current understanding of how the brain works, the science behind Brainbow, the potential applications of connectomics, and the nature of consciousness.

What is Our Current Understanding of How the Brain Works?¶

What is our current of how the brain works? In Prof. Lichtman’s opinion, this question is perhaps best answered through analogy. Imagine you are a mountain climber attempting to summit Mount Everest. After climbing just three feet, how much progress have you made? Relative to the starting point, it might seem infinite, but in reality, it’s a very small fraction of the journey. Similarly, when it comes to understanding the brain in complete detail, we don’t even know how tall the metaphorical mountain is. Despite this immense challenge, scientists have still made significant strides in uncovering much of how our neurobiology works.

The basic anatomy of the brain consists of: X Glial Cells > N Neurons.
$\quad$Glial cells support neural function,
$\quad$but Neurons perform the processing and are the key.

The basic function of the brain is to:
$\quad$a. receive input from sensory organs,
$\quad$b. process input information,
$\quad$c. and execute a response to input.

That is essentially what every single neuron does as well, but
$\quad$Neurons receive input at synaptic sites (1–10,000 sites) on the dendrites.
$\quad$$\quad$ONLY IF the total input signal @ synapse $\rightarrow$ <em>local</em> membrane depolarization > some threshold potential $\rightarrow$ signal propagates to the cell body.

$\quad$Incoming signals from dendrites are integrated across the cell body $\rightarrow$ cell body membrane depolarization.
$\quad\quad$ONLY IF depolarization > some threshold potential $\rightarrow$ generation of an output signal at the Axon Hillock and down the axon.
$\quad\quad\quad$ Axon lengths of neurons vary from microns to meters.

When it comes to brain function in general (i.e., response to stimuli), a neuron’s connectivity and the strength of its connections within a group play a critical role. The more connected and influential a neuron becomes, the more essential it is to the function of the neural circuit.

Thus, both a neuron’s role within circuits and its mechanism of operation are crucial to overall circuit function:

$\quad$Wiring (structural connectome) determines the flow of information across neural networks, AND
$\quad$Programming (functional connectome) determines a neuron’s response to stimuli by modulating its excitability or inhibition.

$\because$ A neuron’s sensitivity (i.e., synaptic strength) and response (output) can change—becoming more excitable or sensitized—even without changes to the wiring itself. This is influenced by experience (activity), meaning each neuron’s programming is unique due to variability in experience.

We do not fully understand how neurons communicate. Some neurons respond to excitation with a single action potential, while others respond with bursts of multiple action potentials. The strength of excitatory input signals is encoded in the frequency of action potentials, akin to switching between AM (amplitude modulation) and FM (frequency modulation) in radio. Input is encoded in output frequency.

These differences in input-output modulation depend on the specific types of channels present in the neuron’s membrane, which regulate ion flow and ultimately determine signal properties. This membrane system is highly complex and nonlinear.

In nature, if something can be useful, evolution has likely taken advantage of it. However, it’s not designed to be understood—it just needs to work.

Modeling membrane dynamics is extremely complicated. Therefore, it’s often easier to model a neuron’s response through direct stimulation, such as step-function depolarizations.

The human brain contains an estimated 86 billion neurons. Each neuron forms connections ranging from a few to tens of thousands with other neurons, resulting in trillions of synapses. Interestingly, our brains are neither particularly large nor do they contain an unusually high number of neurons compared to other animals. We are encephalized however, meaning we have a relatively large brain in proportion to our body size.

In addition, compared to other animals, humans have a significant amount of association cortex, which is primarily involved in cognitive processing. The brain’s functional capacity, appears to depend on both the number and size of neurons. Importantly, more or bigger is not always better.

According to Lichtman, there is no magic involved in understanding what a human being is—apart from the enormous complexity of the brain. However, the ability to "understand" depends greatly on how one defines the term.

I think most people’s understanding of the word "understand" implies a shorthand—a compressed version of complexity—where, once you grasp the gist of something, you no longer need the details because now you "get it."

I propose an alternative: certain things in the world, are in their most concise form, and not simplifiable.

If there were a simpler state, the brain would already exist in it.

How to Reconstruct the Structural Connectome¶

Alt Text
Figure 1 – 50 of largest neurons in the fly’s brain connectome. source

The Human Connectome Project mapped the structural (wiring) and functional (information flow between areas) aspects of the human brain in a macro connectome—also known as the Projectome—in 2012. However, to understand how neural information translates into behavior, it is necessary to examine the structural and functional microwiring, which constitutes the official Connectome.

In general, this process requires two key techniques: Brainbow and serial section electron microscopy. The procedure begins by preserving the brain in a paraformaldehyde resin at the time of death * to minimize neural network decay. The brain is then sliced into thin sections, 10–30 nm thick, using a diamond blade. These slices are stained with Brainbow, a multiplex staining protocol that enables the resolution and visualization of individual neurons at the synapse level across each slice (visit to understand why this is hard). The stained slices are imaged in series using electron microscopy, allowing the projections of each neuron to be traced across slices. When the images are stacked, they produce a nanometer-resolution 3D reconstruction of all neural wiring.

Despite a large and growing body of knowledge on neural signaling, we currently lack the integration necessary for comprehensive functional connectome modeling.

* This presents ethical challenges in obtaining a complete human brain for scanning.

Connectomics¶

The first complete structural connectome was mapped for a small nematode worm, C. elegans, which has only 300 nerve cells. This effort took 10 years. More recently, in 2024, the structural connectome of the fruit fly (Drosophila melanogaster) was published (figure 1). The next planned milestone is mapping the mouse brain, a project expected to take 5–7 years. Mapping a whole mouse brain will require terabytes of data per section, posing a significant challenge as these terabytes quickly scale to petabytes or even exabytes. Currently, Prof. Lichtman and his colleagues are developing the tools necessary to handle, store, and integrate this immense volume of data.

The human brain, being orders of magnitude larger and more complex than a mouse brain, will generate data on the scale of zettabytes—equivalent to the total digital content of the World Wide Web in a single year.

At present, we simply lack the capacity to process and manage this amount of information.

The ultimate goal of the connectome is to functionally model the human brain, allowing sensory input sent along sensory fibers to result in motor behavior output. However, a major challenge lies in the complexity of a brains neural network, where nuerons can form thousands to tens of thousands of connections and participate in numerous circuits. In addition to processing information, the brain must also store it, adding another layer of complexity.

This challenge is further compounded by latent influences not captured in the structural diagram, such as synaptic strength, the nonlinear responses of cells, the timing of inputs that activate cells (resulting in excitatory or inhibitory effects), and the influence of modulatory neurotransmitter inputs.

While there is still much to be learned from the structural connectome alone, true brain simulations will require integrating with the dynamic processes of information processing that govern input-to-response pathways. There is still much work to be done before this can be achieved.

While the connectomes of worms and fruit flies have some relevance to humans, they are primarily valuable to neuroscience researchers working with these animal models. For instance, despite the fruit fly connectome being published only in mid-2024, several studies have already utilized it to explore a range of topics, including the discovery of new circuits (Seung, 2024), elucidation of circuit functions (Sapkal et al., 2024), brain modeling (Shiu et al., 2024), and brain dynamics (Pospisil et al., 2024).

The mouse connectome is anticipated to have even greater utility. Furthermore, the connectome could prove beneficial for advancing artificial neural network architectures. Its first direct human application may lie in studying psychiatric, developmental, and cognitive disorders. There is a possibility that these conditions stem from some form of miswiring in the brain—but what kind of miswiring? Nobody knows. And how could we know without the connectome?

The Easy and Hard Problem of Conciousness¶

The Easy Problem of Consciousness = How do sensory inputs give rise to motor reactions and behavior.

The Hard Problem of Consciousness is how do we get our inner experiences, how do we know what it’s like to see the color red, or taste something spicy.

When it comes to consciousness, Prof Lichtman is of the opinion that every living thing is conscious. He feels that because humans are so fixated on describing the world with language that we end up with puzzles that are more linguistic problems than brain problems. His best guess currently is that neurons operate to survive; they are like a single-celled organism. In doing so (trying to survive), which involves making connections and coopperating with other neurons, and the process of performaning their survival tasks, complex neural function emerges.

That’s just what they’re doing; they just know that if they don’t do that, they’re going to be punished and die

December 10 2024

admin Neuromorphic Computing & Engineering Adaptive Learning, Artificial Neural Networks, Brain-Inspired Architecture, Low Power Consumption, Memristors, neuromorphic computing, Neuromorphic Hardware, paper review, Parallel Processing, Pattern Recognition, spiking neural networks 0

129_p2_pr_Extensive Analysis of Neuromorphic Computing

Paper Review:¶
An Extensive Analysis of Neuromorphic Computing¶

source: Vajpayee, Amit, Palak Preet Kaur, Ankit Sharma, and Santosh Varshney. “An Extensive Analysis of Neuromorphic Computing.” In 2024 International Conference on Advances in Computing Research on Science Engineering and Technology (ACROSET), 1–5. Indore, India: IEEE, 2024. https://doi.org/10.1109/ACROSET62108.2024.10743880.

This paper is an easy entry into the field of Neuromorphic Computing. Covering a very high level overview of the topic. The overall premise is that Neuromorphology (inspires) $\rightarrow$ Neuromorphic computing (NMC).

Neuromorphic Computing (NMC) = third-generation Artificial Neural Network (ANN) technology, with the ulitmate goal of

creating high-performance cognitive systems that emulate the brain's unparalleled capabilities in learning, decision-making, and adaptability..

The authors recognize Rodney Douglas and Misha Mahowald two key pioneers whose work in the 1990s and early 2000s laid the foundation for neuromorphic hardware and architectures. Their contributions focused on mimicking the physical structure and function of the brain's neural circuits, creating systems that were not just biologically inspired but also capable of performing brain-like computations with efficiency and robustness. The paper also does a good job in my mind, highlighting the benefits and challenges of NMC systems over traditional von Neumann computing architectures, with a strong emphasis on hardware considerations.

Neuromorphic Computing (NMC) addresses the problem of brain-like computation and efficiency through two primary approaches:

Modeling the Brains Physical Structure

This involves designing hardware that closely mimics biological neural networks, including synaptic connections and signal propagation.

Translating Cognitive Tasks into Algorithms:

This involves designing novel algorithms to function on top of these NMC networks

Key Features of Neuromorphic Computing.¶
Neuromorphic systems offer two key advantages:

Massive Parallelism : processing information in parallel, mimicking the distributed architecture of the brain’s neural networks

Low Power Consumption : emulating the energy-efficient mechanisms of synaptic transmission $\rightarrow$ significantly reduced energy requirements compared to traditional computing.

NMC holds great promise, particularly in applications requiring low-energy, high-efficiency processing where pattern recognition, decision-making, and AI processes are required. Ideal for application in:

Artificial Intelligence Systems : Advanced pattern recognition and decision-making.

Adaptive Learning in Robots : Systems capable of learning and adapting post-deployment.

Diagnostics in Medicine : Enhancing medical imaging and predictive analytics.

Advantages of NMC compared to Traditional AI systems.¶

Energy efficiency. Ideal for energy-critical applications like edge devices

Fault Tolerant.These systems are resilient to local failures, mimicking the brain’s ability to reroute processes in case of damage.

Scalability.Their modular, distributed design allows for seamless scaling to handle increasingly complex tasks.

Speed. Neuromorphic systems execute tasks faster due to their parallel processing capability.

Pattern Recognition.Exceptional at recognizing complex patterns in data, including image and speech recognition.

*edge device:= a type of hardware that processes data at or near the location where it is generated, rather than relying on centralized systems. These devices are typically part of an edge computing architecture, where computing, storage, and decision-making occur close to the "edge" of the network to reduce latency, bandwidth usage, and energy consumption

Neuromorphic Hardware¶

Neuromorphic Chips and Architecture, Chips mimic neural architectures for efficient computations by mimicking the connectivity and operations of biological neurons.

Memristors, Memristors are energy-efficient, non-volatile memory devices critical to neuromorphic systems. They act as resistive switch cells capable of modeling synapses between neurons.

Neuromorphic Sensors and Interfaces, enable compact, adaptable, and intelligent biosensors capable of sensing, recognizing, and making decisions.

The memristor stands out as a pivotal component, a metal oxide (TiN/HfOx/AlOx/Pt) resistive switching mechanism to replicate synaptic behavior. Its ability to store presented patterns and relationships closely mirrors Hebbian learning—“neurons that fire together wire together.”

Neuromorphic Algorithms¶
Neuromorphic algorithms are designed to accelerate the neural network processing in the context of Spiking Neural Networks (SNNs).

SNNs transmit information as discrete spikes (1s and 0s), closely emulating biological neurons.

These algorithms prioritize real-time, memory-efficient computation to optimize the relationship between processing and storage.

Challenges and Limitations of Neuromorphic Computing¶
Despite its promise, Neuromorphic Computing faces significant barriers to widespread adoption:

Complexity : The intricate designs required to mimic biological systems make implementation and optimization challenging.,

Cost : Design and manufacturing of NMC systems remain expensive due to the specialized hardware requirements like custom chips and memristors.,

Lack of Standards : Field lacks standardized benchmarks and performance metrics which hinders comparison and evaluation between systems in application.

Limited Application Domains : NMC allone will likely not be suitable for all types of computing work.

Accuracy and Precision : Neuromorphic systems have lower accuracy and precision compared to traditional neural networks. Particularly in critical computational tasks.

October 1 2024

admin Machine Learning & Artificial Intelligence Artificial Intelligence (AI), Biological Neural Networks, Brain-Inspired Architecture, Crossbar Arrays, Deep Learning vs. SNNs, Energy-Efficient Computing, Fault Tolerance, Future of AI and Computing, Hardware Innovation, Machine Learning Applications, Memristors; Neural Network Hardware, neuromorphic computing, Non-Volatile Memory, Pattern Recognition, Robotics; Edge Computing, Scalability in Computing, Spiking Neural Networks (SNNs) 0

WIHL_ML&AI

Principles from Theory and Fundamentals¶

Machine Learning (ML) is a field of study that uses algorithms to learn patterns from data. An Artificial Neural Network (ANN) is a type of computer architecture that processes data in order to explicitly programmed on how to solve it (see basics of ML and AI.ipynb:Table 1)

An ANN is said to learn $(L)$ from experience $(E)$ for a specific task $(T)$, based on Performance Measure $(P)$, if $P(T)$ improves as $E$ increases where $E$, Experience $\Rightarrow$ is the acquisition of new data representative of T(Data)

$\therefore$ $AI$ := ML optimized ANN capable of high P(T) for a specific Task
Where
$\quad$$\quad$$L$ := optimization of network output with respect to the loss function
$\quad$$\quad$$T$ is some specific algorithmic process
Note $\because$ $T$ is for a specific algorithmic process only $\Rightarrow$ modern (2024) AI systems are not (yet) capable of general optimization $ \&\therefore$ AI $!=$ General AI or General Intelligence but rather very specific task focused systems

The Challenges to AI¶

Despite all the marvelous implementations of AI technology. AI adoption and implementation has some serious challenges to overcome.

1. Semantics
Modern AI systems currently (2024) cannot handle ambiguity, subjectiveness and common-sense (cultural/social sense) oriented tasks, i.e non-algorithmic tasks

2. Power Consumption
Total energy consumption in general is:
TOTAL ENERGY CONSUMPTION = ENERGY TO TRAINING + ENERGY FOR INFERENCE $$E_{total} = ( P_{hardware}\cdot t_{train}) + ( P_{inference}\cdot t_{inference}\cdot N_{inferences}) $$ $\quad$where,
$\quad\quad P_{hardware}$ = Power consumption of the hardware during training
$\quad\quad t_{traim}$ = time taken to train the model
$\quad\quad P_{inference}$ = Power consumption per inference
$\quad\quad t_{inference}$ = time for a single inference
$\quad\quad N_{inference}$ = total number of inferences performed

Modern (2024) large scale, real world application systens (AlphaGo, Alpha Fold, ChatGPT $\dots$), $E_{total}$ is hundreds of killowats\hr of continous electricity use $\equiv$ to an industrial manufactoring factory, but only the size of a large office. This does not inlcude the electricity required to power the cooling and supporting infrastructure

3. Training Time
For large AI models, training can take days to months $\Rightarrow$ training is an energy expensive process $\therefore$ live updating (or minumum day update cadence) is difficult=esxpensive

4. Training Data and Storage
Large AI models require huge amounts of highly specific and structured data (ranging from terabytes to petabytes), spanning as much of the experience $(E)$ sapce possible within a task $(T)$ performance. The storage of this data is no easy task either.

The Basic Cell¶

The fundamental unit of any ANN = Basic Cell = One node Feed Forward Network (FFN) = Perceptron (Figure 1). A perceptron is the simplest type of neural network, where information flows in one direction—from input to output—without loops. Inspired by how neurons in the brain work. Modern ANN architectures are considered fully-connected even though with the introduction of layers $\rightarrow$ organization = structure $\rightarrow$ modularity and reduced connectivity $\rightarrow$ higher-order functions $\Rightarrow$ the emergence of apparent intelligence in the system. A Perceptron alone is best suitable for solving linearly separable classification problems —that is, problems where the data can be divided into two classes using a straight line (in 2D), a plane (in 3D), or a hyperplane (in higher dimensions). Eg. Identifying spam by keywords in emails. This is because the perceptron computes a weighted sum of inputs, applies a bias, and passes the result through an activation function (e.g., a step function), which gates the activation in a binary process. This simple mechanism is sufficient to separate data into two groups but for more complex data multi-layer perceptrons (MLPs) or deep neural networks (DNNs) are needed. With the addition of multiple (tens to hundreds) layers its possible to progressively extract higher-level features from the raw input. Eg the early layers in an image recognition DNN might detect edges, while deeper layers might identify shapes, objects, or faces.

Figure 1 – Skematic representation of a Perceptron, equivalent to a single node feed forward ANN.

ANN Structure and Organization : Inference Layer¶
An Artificial Neural Network (ANN) is a simplified computational model designed to mimic the structure and function of neural networks in the human brain. Rather than biological systems, ANNs are implemented in software as organized arrangements of interconnected nodes, often referred to as cells, which are structured into distinct layers (Figure 2). These layers facilitate the flow of information through the network, enabling complex computations.

Fjodor van Veen (2016, 2017) of the Asimov Institute has curated an extensive collection of diagrammatic representations of various ANN architectures and their functions, based on primary literature sources. His work highlights that most modern neural networks are constructed using only a handful of fundamental cell types, which are combined in diverse ways to produce the wide array of architectures we use today.

Figure 2 – A skematic representation of a generic ANN architecture represented in code

The connection between a presynaptic node in one layer and a postsynaptic node in the subsequent layer is often represented using index notation. This notation helps specify the particular relationship:

$i^{th}$ Connection,
of $j^{th}$ node (post-synaptic),
in $L^{th}$ Layer (post-synaptic),
from $k^{th}$ node in $(L-1)$ Layer (pre-synaptic)

The signal strength, $S$, of a connection $i$ to cell $j$, in layer $L$ = product of Input feature $(\theta^{L}_{i,j})$, into $i^{th}$ connection to $j^{th}$ cell, in $L^{th}$ layer AND connection weight $(w^{L}_{i,j})$. This weight determines the relative importance of the connection. Upon initialization of the artificial neural network (ANN), these weights are typically assigned random real values (positive, negative, or zero). $$S_{i} = \theta_{n} \cdot w_{i} \quad\quad\quad (1)$$

A Perceptron aggregates all incoming inputs into a weighted sum — also known as net input, $(z)$. This aggregation includes an activation bias, $b$, a constant that can range depending on the initialization strategy and the optimization process, which allows the network to adjust the output independently of the input. The bias term helps prevent the perceptron from being stuck at output values like zero and can enhance flexibility in modeling complex data
$$z = \sum_{i=1}^{n} S_{i} + b_j= \sum_{i=1}^{n} \theta_{n}w_{i} + b_{j} \quad\quad\quad (2)$$

he net input is transformed into an output value through an Activation Function $(F)$. the classical perceptron introduced by Frank Rosenblatt (1958), the activation function was a step function, producing discrete outputs (e.g., binary classifications like 0 or 1). While step functions work well for simple tasks, modern neural networks—which evolved from perceptrons—use more sophisticated activation functions such as sigmoid, tanh, or ReLU (Rectified Linear Unit). These functions enable the network to model more complex relationships between inputs and outputs, improving the ability to approximate real-world data. $$ F(z) = a \quad\quad\quad\quad (3)$$

Where $a$ is the output of the activation function. During inference this output is either passed to subsequent nodes in the next layer or used as the network’s final output. During the trainig phase it is evaluated in the update layer of the network.

ANN Structure and Organization : Update Layer¶

During the training phase of a neural network, input data is propagated through the perceptron, where its performance is evaluated at the output. The optimization process—central to machine learning—enables the perceptron to independently update its connection weights, $(w_{i,j})$ using input data $(X \in [\vec{x}, \vec{y}] = ((\theta_1,…\theta_n), y)$. This is achieved through iterative adjustments aimed at minimizing the error, as defined by the loss function $\phi$.

The optimization process improves the network’s performance measure, $P(T)$, by applying a learning algorithm that reduces the gradient of the loss function, $\nabla\phi(w,b)$. This gradient descent approach guides the network toward optimal predictions. The step size for each adjustment is determined by the learning rate $(\eta)$ which regulates the rate of convergence:
$\quad$ Smaller steps $(\eta)$ : Enable finer adjustments, leading to higher accuracy but slower convergence.
$\quad$ Larger steps $(\eta)$ : Speed up training but risk overshooting and reduced accuracy.
The weight update rule, which lies at the heart of the training loop, is expressed as:
$$w^{*}_{i,j} = w_{i,j} – \nabla\phi(w,b) \quad\quad\quad\quad (4)$$

Here $w^{*}_{i,j}$. represents the updated weight, and $\phi$ quantifies the error between the network’s predictions and the target outcomes. By iteratively minimizing $\phi$ the network becomes increasingly adept at generating accurate predictions.

Keynote¶

In this article the Activation Funtion,$(F)$, and the loss function $(\phi)$ were not discussed in any detail. A large deal of the complexity and intricacies surrounding the details of the Training and Inference process depend on these functions, and so they will be covered in more detail at another time.

Sources¶

Sources … …
[1] Dive in Deep Learning, E-Book
[2] The Assimov Institute: Project > Neural Network Zoo Project

Aknowledgements¶

Big thank you to everyone at OpenAI, ChatGPT was super helpful in brainstorming, editiing, and preliminary research.